Gewicht allgemein, ungefederte Massen, jetzt also: rotierende Massen. Damit soll es aber dann auch, zumindest bis auf weiteres, gut sein – aber die rotierenden Massen zu vernachlässigen wäre auch nicht fair, vor allem vor dem Hintergrund der Laufradgrößen-Diskussion.
Der korrekte physikalische Hintergrund im Zusammenhang mit rotierenden Massen heißt übrigens: Trägheitsmoment. Moment, da klingelt’s, wie beim Drehmoment auch geht es hier um ein Rotationsphänomen. Das Trägheitsmoment eines rotierenden Körpers hängt von seiner Massenverteilung ab: Sitzt das Gewicht weiter außen, vergrößert sich das Trägheitsmoment. Sitzt das Gewicht weiter innen, verringert es sich. Generell ist ein kleineres Trägheitsmoment erstrebenswert, wenn man beschleunigen möchte. Ein hohes Trägheitsmoment ist aber auch nicht zwangsläufig verkehrt, es hilft zum Beispiel Schwung zu behalten oder sich nicht aus der Spur werfen zu lassen.
Aber: Der Reihe nach. Beim Laufrad sitzt schon Mal die meiste Masse ganz außen. Im Bereich der Speichen ist ziemlich wenig los, und in der Nabe ist ganz mittig auch nochmal etwas Masse platziert. Das spannende ist jetzt: Der Einfluss der Masse auf das Trägheitsmoment nimmt nach außen hin nicht linear zu, sondern quadratisch. Soll heißen: Wechselt man von einem 27,5“-Laufradsatz auf einen gleich schweren 29“ Laufradsatz, so hat dieser nicht das gleiche Trägheitsmoment – denn die Masse sitzt ja weiter außen. Er hat auch nicht ein um 6 % größeres Trägheitsmoment (das entspräche dem Durchmesser-Unterschied), sondern ein um ca. 12 % Größeres Trägheitsmoment. An dieser Stelle kann man sicher diskutieren, ob 12 % sich hier oder dort spüren oder eben nicht spüren lassen, aber es geht ja noch weiter: Eine größere Felge ist ja zumeist nicht gleich schwer, sondern gewöhnlich schwerer; das gleiche gilt für Reifen, Schlauch (so vorhanden) und Speichen. Bei gleichen Materialstärken steigt das Gewicht beim Umstieg von 27,5“ auf 29“ von beispielsweise 1880 g auf 2000 g. Die Kombination aus größerem Gewicht und größerem Durchmesser führt also tatsächlich zu einem 20 % größeren Trägheitsmoment.
Das Trägheitsmoment gibt an, wie schwierig oder leicht es ist, einen Körper – in unserem Fall ein Rad – anzudrehen oder abzubremsen. Kennt man das Trägheitsmoment um die entsprechende Achse, kann man direkt berechnen, welches Drehmoment für eine gewisse (Winkel-)Beschleunigung benötigt wird, oder, weniger kryptisch formuliert: Wie stark wir in die Pedale treten müssen, um das Rad in Drehung zu versetzen. Was wir hier sehen: Das Trägheitsmoment steigt stärker als die Masse, und in Konsequenz beschleunigt ein 29er gleichen Gewichts träger als ein 27,5“-Bike. Aber, und das ist immer wichtig zu sehen: Der gleiche Effekt ist nicht nur Feind, sondern auch Freund: Sind die größeren Räder nämlich einmal beschleunigt, so behalten sie ihre Rotation auch lieber bei. Ein Blick auf die Energiebilanz zeigt, dass das Ganze in Summe egal ist – nur die Änderungen eben langsamer, träger ausfallen, was sich dann direkt als trägeres (oder gleichmäßigeres) Verhalten bemerkbar macht. Übrigens: Größere Räder drehen sich natürlich auch langsamer, was ihren Drehimpuls wieder verringert. Der Effekt des größeren Trägheitsmoment überwiegt aber, da die nach außen wandernden Massenanteile quadratisch eingehen – der Durchmesser wirkt sich dagegen nur linear auf die Winkelgeschwindigkeit aus.
Richtig spannend wird es aber erst dann, wenn wir die rotierenden Massen (nennen wir sie einfach mal „Kreisel“) nicht nur um eine Achse drehen lassen. Aufgrund des Kreiseleffekts (siehe Drallsatz) der Präzession weicht ein rotierendes Rad einer Drehung um eine Achse durch eine Drehung um eine Achse senkrecht dazu aus. Am einfachsten kann man sich das als Fahrradfahrer natürlich am Fahrrad vorstellen, ansonsten führen die verschiedenen Drehmomente und Drehachsen eher zu Verwirrung. Beispiel Nummer 1, was passiert wenn wir das Fahrrad neigen?
- Das Fahrrad fährt, die Räder drehen sich in Fahrtrichtung.
- Das Fahrrad neigt sich, die drehenden Räder werden quer zur Fahrtrichtung geneigt.
- Das Vorderrad weicht dieser Fahrrad-Neigung durch eine Drehung der Federgabel (näherungsweise senkrecht zur Fahrtrichtung) aus.
Das kennen wir aus der praktischen Erfahrung: Sein Fahrrad zu neigen leitet eine Kurve ein. Gleichzeitig ist das einer der zwei Gründe dafür, warum ein Fahrrad ab einer gewissen Geschwindigkeit stabil fährt, sich also auch ohne Fahrer wieder aufrichtet: Schließlich führt ein Lenken in Richtung der Neigung dazu, dass eine Kurve eingeleitet wird, die den Fahrradschwerpunkt wieder aufrichtet, was dann zu der Pendelfahrt um die Mittellage führt, die ein fahrerloses Fahrrad vollführt.
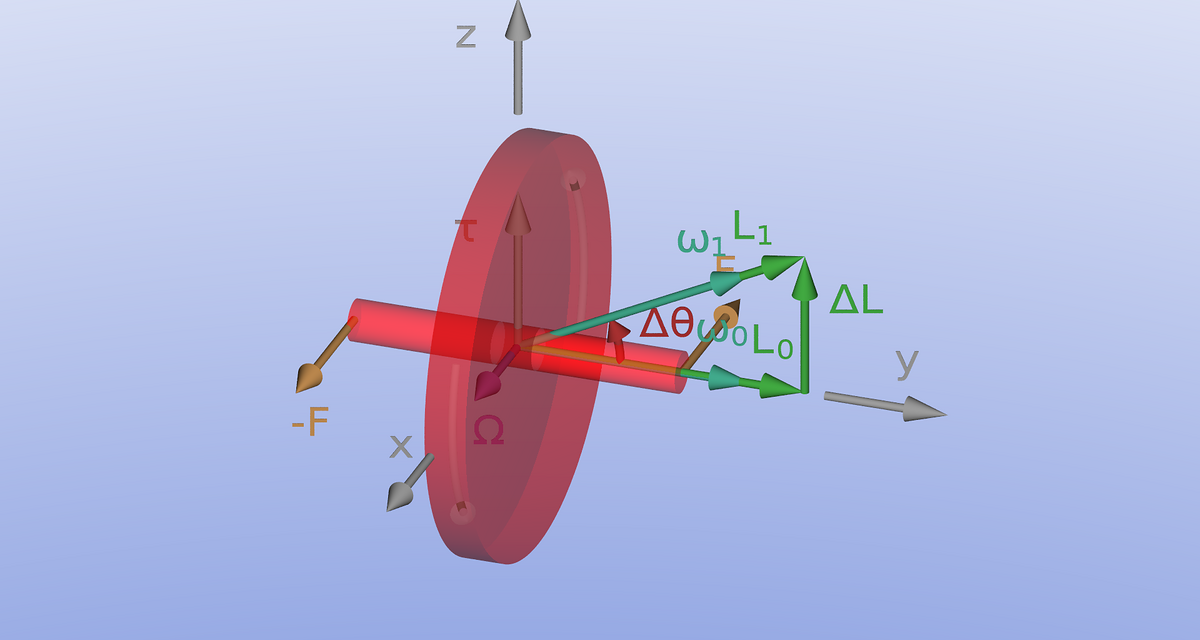
Diese Kreiseleffekte lassen sich an einem physikalischen Experiment relativ spannend und vor allem unintuitiv zeigen: Ein ausreichend schnell rotierendes Rad kippt bei einseitiger Fixierung nicht durch die Schwerkraft nach unten, sondern weicht stattdessen durch eine Drehung aus:
Diese Momentenreaktion findet übrigens auch dann statt, wenn man das Vorderrad einlenkt – hier kommt Beispiel Nummer 2:
- Das Fahrrad fährt, die Räder drehen sich in Fahrtrichtung.
- Der Lenker wird eingedreht, die drehenden Räder werden quer zur Fahrtrichtung gedreht.
- Das Fahrrad weicht dieser Vorderrad-Drehung durch eine Neigung aus.
Dieser Effekt führt dazu, dass man mit einem Fahrrad keine Kurve fahren kann, indem man einfach nur am Lenker dreht – ohne Neigung keine Kurvenfahrt! Aber zurück zum Thema rotierende Massen: Steigt der Drehimpuls (durch größeren Durchmesser oder größere Masse) so ist es nicht nur schwieriger die Drehgeschwindigkeit zu ändern, sondern auch schwieriger, das Rad zu neigen oder zu lenken.
Das ist der Grund, weshalb sich ein 29er träger bewegen lässt als ein Bike mit kleineren Rädern. Oder ein Bike mit leichteren Rädern leichter als eines mit schwereren Rädern. Aber erneut gilt: Trägheit ist nicht nur schlecht, ein Rad mit größerem Drehimpuls lässt sich auch weniger gern durch Schlaglöcher und Wurzeln aus der Bahn werfen, es fährt einfach gern in seiner bisherigen Richtung weiter.
Größeres Trägheitsmoment gleich schlechtere Laufradgröße? Natürlich nicht! Twentyniner haben in vielerlei anderer Hinsicht Vorteile. Wie aber auch bei der ungefederten Masse soll auch hier das Fazit heißen: Wenn Gewicht sparen, dann am besten am Rad – denn das ist sowohl ungefederte als auch rotierende Masse. Blöd nur, dass das alles natürlich nichts hilft, wenn man mit einem leichten Reifen dann viele Plattfüße hat.
Alle Artikel der Dreh-Momente-Reihe
- Dreh-Momente am Dienstag: Junggesellenabschied im Bikepark
- Dreh-Momente am Dienstag: Handy am Steuer des Geländerads!
- Dreh-Momente am Dienstag: Können Carbon-Fahrräder recycelt werden?
- Dreh-Momente am Dienstag: Allrad-Antrieb am Fahrrad
- Dreh-Momente am Dienstag: Die Fahrradrahmen-Produktion der Zukunft
- Dreh-Momente am Dienstag: Triathlonrad meets XC-Fully
- Dreh-Momente am Dienstag: Von Bremsen und Lenkern
- Dreh-Momente am Dienstag: Worauf legt man eigentlich ein Mountainbike aus?
- Dreh-Momente am Dienstag: Wie optimiert man eine Luftfederkennlinie? Gastbeitrag von Bommelmaster
- Dreh-Momente am Dienstag: Individuelle Sättel durch 3D-Druck
- Drehmomente am Dienstag: Was spricht für Parallelogramm-Federgabeln?
- Dreh-Momente am Dienstag: Aerodynamik auf dem Mountainbike
- Dreh-Momente am Dienstag: Gefahrenherde im Bike-Alltag
- Dreh-Momente am Dienstag: Wie wird eigentlich ein Sattel entwickelt?
- Dreh-Momente am Dienstag: Rotierende Massen
- Dreh-Momente am Dienstag: Ungefederte Massen
- Dreh-Momente am Dienstag: Lasst uns über Gewicht sprechen
- Dreh-Momente am Dienstag: Wie Danny MacAskills neues Santa Cruz Carbon Trial-Bike entstand
- Dreh-Momente am Dienstag: Ergibt es Sinn, ein Fahrrad aus dem Vollen zu fräsen?
- Dreh-Momente am Dienstag: Dämpfung – was ist das eigentlich?
- Dreh-Momente am Dienstag: Warum werden Bremsscheiben so montiert?
- Lenkwinkel am Mountainbike: Flach oder steil – einfach erklärt!
- Dreh-Momente am Dienstag: Wo sind eigentlich die echten Steckachsen hin?



103 Kommentare